10.11 Where are we?
- 10 1 Slope Field Sap Calculus Equation
- 10 1 Slope Field Sap Calculus Calculator
- 10 1 Slope Field Sap Calculus Formulas
Numbers are numbers. Read the section on them again.
Slope Fields Notesheet 02 Completed Notes Slope Field Card Match 02 Solutions Slope Fields Homework 02 - HW Solutions Euler's Method Notesheet 03 Completed Notes Euler's Method Homework 03 - HW Solutions Euler's Method and Slope Fields 04 Coming Soon! All the Things Homework 04 - HW Solutions All the Things Practice 05. Slope fields are visual representations of differential equations of the form dy / dx = f (x, y). At each sample point of a slope field, there is a segment having slope equal to the value of dy / dx. Any curve that follows the flow suggested by the directions of the segments is a solution to the differential equation. If we want to find the slope of the line tangent to the graph of at the point, we could evaluate the derivative of the function at. On the other hand, if we want the slope of the tangent line at the point, we could use the derivative of. However, it is not always easy to solve for a function defined implicitly by an equation. Calculus 10th Edition answers to Chapter 1 - Limits and Their Properties - Section Project - Graphs and Limits of Trigonometric Functions - Page 90 d including work step by step written by community members like you. Textbook Authors: Larson, Ron; Edwards, Bruce H., ISBN-10: 1-28505-709-0, ISBN-13: 978-1-28505-709-5, Publisher: Brooks Cole.
Functions are sets of (argument, value) pairs of numbers . They are often described by formulae which tell us how to compute the value from the argument. Only one value is allowed for each argument. The formulae you will usually encounter start with the identity function, the exponential function and the sine function, and are defined by applying arithmetic operations, substitution and inversion in some manner to them.
The derivative of a function at any argument is the slope of the straight line it resembles near that argument, if that slope is finite. The straight line it resembles near that argument is called the tangent line to the function at that argument and the function describing that line is called the linear approximation to the function at that argument. If the function does not look like a straight line near an argument, (has a kink or a jump or crazy behavior there) it is not differentiable at that argument.
There are straightforward rules for calculating derivatives of the identity, sine and exponential functions, and for computing derivatives of combinations of these obtained by applying arithmetic operations, substitution and inversion in some manner to them.
Thus we have means to obtain formulae for the derivative of all functions of the kind described above. The rules appear below.If you are not comfortable with them, practice!
Armed with a spreadsheet, you can plot functions and determine their derivatives with great accuracy, most of the time, with little effort.
10 1 Slope Field Sap Calculus Equation
What else should I know at this point?
First, you should feel comfortable with calculating or computing derivatives numerically.
So far, all we have said about the exponential function is the statements that its value at argument (0) is (1), and it is its own derivative everywhere. And the sine function is (0) at argument (0) and has derivative that is the sine of the argument complement to it.
You would be well advised to review the properties of the sine and the other trigonometric functions and the exponential. These are described in section T.
OK, what can we do with this?
The two major applications of differentiation are modeling phenomena, and solving equations.
Do I really expect to do these things?

You cannot ever be called on to do either of these things if you have no idea how to do them. Similarly you will only rarely be asked to cross a road if you never learned how to walk. Once you know about these things, all sorts of possibilities open up that you can begin to handle.
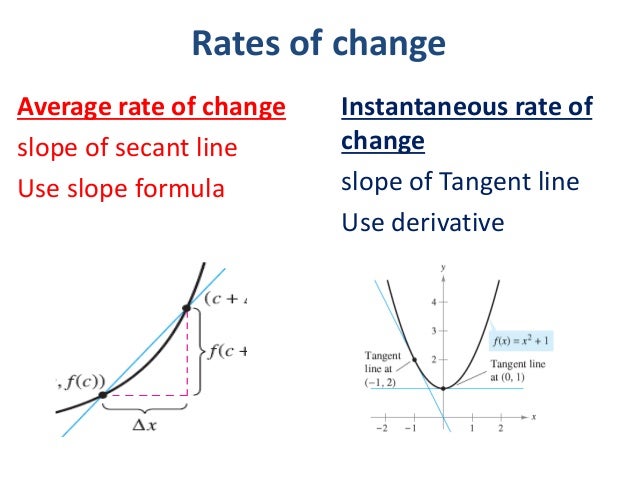
Once a model of a phenomenon has been constructed, you want to be able to deduce the consequences of the model. This involves getting back from derivatives or equations involving derivatives to the functions whose derivatives they are.
The processes of going from a derivative back to a function is sometimes (rarely) called anti-differentiation, and usually called integration or quadrature (also a rare name). Going from an equation involving derivatives to the original function is called solving (or integrating) a differential equation.

In the next section we will describe a way to use differentiation to solve non-linear equations involving one variable, and other methods for doing so as well. Then we will discuss integration and you will learn how to do it, where possible, both numerically and by formula. We will then give examples of use of derivatives in modeling real world situations. Finally we will examine how to solve differential equations numerically, and so discover the implications of such models.
Is this all I have to know about calculus?
The answer depends on your goals.
If you seek only a qualitative notion of what calculus is about, you can quit when you are satisfied that you have one. At this point we have only discussed differentiation. The inverse operation to taking the derivative of a function is of equal interest and is yet to come.
If your goal is to understand the language of science, in which models of change appear everywhere, this is a good start but there is more, in two directions.
First, we live in a world in which it takes three numbers to describe the location of a point in space; six numbers to describe the location of two points, and so on; and people often want to model motion in space. Thus we need to be able to examine change when we are dealing with several or many variables at a time. So we need to be able to extend the notion of differentiation to the analog of functions which depend on more than one variable. Doing this means extending the notion of derivative to sets of argument-value pairs for which the arguments and/or the values are sequences of numbers rather than single numbers. The study of such things is called Multi-Variable Calculus.
Fortunately it is possible to make the desired extension in a way which allows you to exploit your ability to differentiate in one dimension to get results in higher dimensions. You have to learn some new concepts but the work of differentiating is the same. This subject largely consists of the introduction of new multi-dimensional concepts, and description of how they can be calculated or computed by the techniques of one dimensional calculus.
Second, there is a large amount of lore about differential equations that has developed over the years as people have studied equations that arise in real world applications. In the past, numerical methods, like those you can now apply, were completely impractical, and special methods were found to solve many classes of equations. These methods were also valuable for allowing people to get an idea of the solutions of more complicated equations without actually solving them.
The fact that these methods are adequate for solving very important problems in a number of fields, and that they provide intuition about many other equations means that they are still of interest and worth studying today.
Perhaps the first goal that is well worth your pursuing is to gain the possibility of understanding scientific literature. Papers in science and engineering use notions and notations of derivatives and integrals incessantly, and if these buffalo you, you can get nowhere with reading the literature. Once you are comfortable with the concepts of calculus and their notations, this difficulty disappears.
Enough vague nonsense!
10.12 Algebraic Rules For Differentiation. (And how to deduce them)
Facts 0: The derivative of a straight line function (ax) is the slope of the line it represents which is (a). A constant function has derivative (0). This mean from the original formula, the (x) is replaced by a (1) and any constant term is omitted. By definition we have (frac{de^x}{dx} = e^x) and we have (frac{dsin(x)}{dx} = cos(x) = sin(x + frac{pi}{2})).
Basic Rule 1: To compute the derivative of a function having several occurrences of the variable (let it be (x)), take the derivative contribution from each occurrence separately, treating the others as constant, and add all these up
Consequences:
Sum Rule: (frac{d(f(x)+g(x)}{dx} = frac{df(x)}{dx} + frac{dg(x)}{dx})
Product Rule: (frac{d(f(x)g(x)}{dx} = left(frac{df(x)}{dx}right)g(x) + f(x)left(frac{dg(x)}{dx}right))
Power Rule: (frac{d(x^k)}{dx} = kx^{k-1}) ((k) different (x)'s are replaced by (1) separately and summed)
Quotient Rule: (frac{d(1/f(x))}{dx} = -frac{df(x)/dx}{f(x)^2}). (differentiate both sides of the equation (f(x)left(frac{1}{f(x)}right) = 1).)
Basic Rule 2: The derivative of a function of a function, (f(g(x))), is the product of (frac{df}{dg}) evaluated at (g = g(x)) and (frac{dg(x)}{dx}). This is called the chain rule, and it follows directly from the definition of the derivative when expressed as a ratio of changes.
Consequences:
The Inverse Rule. The inverse is defined by: If (y = f(x)) then (x = f^{-1}(y)),
Since (frac{dy}{dx} = f'(x)), (frac{dx}{dy} = frac{1}{f'(x)}) which means (after switching variable names) (frac{df^{-1}(y)}{dx} = frac{1}{f'(y)}), evaluated at (y = f^{-1}(x)).
The Fundamental Theorem: The derivative of a definite integral with respect to its upper limit is the integrand evaluated there.
If you are comfortable with these facts, are not cowed by numerical computation, and make efforts to study your mistakes so that you have hope of not making them again, you are where you want to be concerning differential calculus in one dimension.
Exercise: Imagine you are teaching a course in calculus. Make a list of 10 questions that you would find hardest to answer with regard to the material in the first 9 chapters. I believe that making up questions is a more challenging endeavor than is answering them.
Coordinate systems are tools that let us use algebraic methods tounderstand geometry. While the rectangular(also calledCartesian) coordinates that wehave been using are the most common, some problems are easier toanalyze in alternate coordinate systems.
A coordinate system is a scheme that allows us to identify any pointin the plane or in three-dimensional space by a set of numbers. Inrectangular coordinates these numbers are interpreted, roughlyspeaking, as the lengths of the sides of a rectangle. In polarcoordinates a point in the plane is identified by a pair of numbers $(r,theta)$.The number $theta$ measures the angle between the positive$x$-axis and a ray that goes through the point,as shown in figure 10.1.1; the number$r$ measures the distance from the origin to thepoint. Figure 10.1.1 shows the point withrectangular coordinates $ds (1,sqrt3)$ and polar coordinates $(2,pi/3)$, 2 units from the origin and $pi/3$ radians from thepositive $x$-axis.
Just as we describe curves in the plane using equations involving $x$and $y$, so can we describe curves using equations involving $r$ and$theta$. Most common are equations of the form $r=f(theta)$.
Example 10.1.1 Graph the curve given by $r=2$. All points with $r=2$ are atdistance 2 from the origin, so $r=2$ describes the circle of radius 2with center at the origin.
Example 10.1.2 Graph the curve given by $r=1+costheta$. We first consider$y=1+cos x$, as in figure 10.1.2. As $theta$ goesthrough the values in $[0,2pi]$, the value of $r$ tracks the value of$y$, forming the 'cardioid' shape of figure 10.1.2.For example, when $theta=pi/2$, $r=1+cos(pi/2)=1$, so we graph thepoint at distance 1 from the origin along the positive $y$-axis, whichis at an angle of $pi/2$ from the positive $x$-axis. When$theta=7pi/4$, $ds r=1+cos(7pi/4)=1+sqrt2/2approx 1.71$, and thecorresponding point appears in the fourth quadrant. This illustratesone of the potential benefits of using polar coordinates: the equationfor this curve in rectangular coordinates would be quite complicated.
Each point in the plane is associated with exactly one pair of numbersin the rectangular coordinate system; each point is associated with aninfinite number of pairs in polar coordinates. In the cardioidexample, we considered only the range $0le thetale2pi$, andalready there was a duplicate: $(2,0)$ and $(2,2pi)$ are the samepoint. Indeed, every value of $theta$ outside the interval $[0,2pi)$duplicates a point on the curve $r=1+costheta$ when$0letheta< 2pi$. We can even make sense of polar coordinates like$(-2,pi/4)$: go to the direction $pi/4$ and then move a distance 2in the opposite direction; see figure 10.1.3. As usual, a negative angle $theta$ means an anglemeasured clockwise from the positive $x$-axis. The point infigure 10.1.3 also has coordinates$(2,5pi/4)$ and $(2,-3pi/4)$.
The relationshipbetween rectangular and polar coordinates is quite easy tounderstand. The point with polar coordinates $(r,theta)$ hasrectangular coordinates $x=rcostheta$ and $y=rsintheta$; thisfollows immediately from the definition of the sine and cosinefunctions. Using figure 10.1.3 as anexample, the point shown has rectangular coordinates $ds x=(-2)cos(pi/4)=-sqrt2approx 1.4142$ and $ds y=(-2)sin(pi/4)=-sqrt2$. This makes it very easy to convertequations from rectangular to polar coordinates.
Example 10.1.3 Find the equation of the line $y=3x+2$ in polarcoordinates. We merely substitute: $rsintheta=3rcostheta+2$, or $ds r= {2over sintheta-3costheta}$.
Example 10.1.4 Find the equation of the circle $ds (x-1/2)^2+y^2=1/4$ in polarcoordinates. Again substituting:$ds (rcostheta-1/2)^2+r^2sin^2theta=1/4$. A bit of algebra turns thisinto $r=cos(t)$. You should try plotting a few $(r,theta)$ values toconvince yourself that this makes sense.
Example 10.1.5 Graph the polar equation $r=theta$. Here the distance fromthe origin exactly matches the angle, so a bit of thought makes itclear that when $thetage0$ we get the spiral of Archimedes in figure 10.1.4. When $theta< 0$, $r$ is alsonegative, and so the full graph is the right hand picture in thefigure.
Converting polar equations to rectangular equations can be somewhattrickier, and graphing polar equations directly is also not always easy.
Example 10.1.6 Graph $r=2sintheta$. Because the sine is periodic, we knowthat we will get the entire curve for values of $theta$ in$[0,2pi)$. As $theta$ runs from 0 to $pi/2$, $r$ increases from 0to 2. Then as $theta$ continues to $pi$, $r$ decreases again to0. When $theta$ runs from $pi$ to $2pi$, $r$ is negative, and itis not hard to see that the first part of the curve is simply tracedout again, so in fact we get the whole curve for values of $theta$in $[0,pi)$. Thus, the curve looks something likefigure 10.1.5. Now, this suggeststhat the curve could possibly be a circle, and if it is, it wouldhave to be the circle $ds x^2+(y-1)^2=1$. Having made this guess, wecan easily check it. First we substitute for $x$ and $y$ to get$ds (rcostheta)^2+(rsintheta-1)^2=1$; expanding and simplifyingdoes indeed turn this into $r=2sintheta$.
Exercises 10.1
10 1 Slope Field Sap Calculus Calculator
Ex 10.1.1Plot these polar coordinate points on one graph:$(2,pi/3)$, $(-3,pi/2)$, $(-2,-pi/4)$, $(1/2,pi)$, $(1,4pi/3)$, $(0,3pi/2)$.
Find an equation in polar coordinates that has the samegraph as the given equation in rectangular coordinates.
Ex 10.1.2$ds y=3x$(answer)
10 1 Slope Field Sap Calculus Formulas
Ex 10.1.3$ds y=-4$(answer)
Ex 10.1.4$ds xy^2=1$(answer)
Ex 10.1.5$ds x^2+y^2=5$(answer)
Ex 10.1.6$ds y=x^3$(answer)
Ex 10.1.7$ds y=sin x$(answer)
Ex 10.1.8$ds y=5x+2$(answer)
Ex 10.1.9$ds x=2$(answer)
Ex 10.1.10$ds y=x^2+1$(answer)
Ex 10.1.11$ds y=3x^2-2x$(answer)
Ex 10.1.12$ds y=x^2+y^2$(answer)
Sketch the curve.
Ex 10.1.13$ds r=costheta$
Ex 10.1.14$ds r=sin(theta+pi/4)$
Ex 10.1.15$ds r=-sectheta$
Ex 10.1.16$ds r=theta/2$, $thetage0$
Ex 10.1.17$ds r=1+theta^1/pi^2$
Ex 10.1.18$ds r=cotthetacsctheta$
Ex 10.1.19$ds r={1oversintheta+costheta}$
Ex 10.1.20$ds r^2=-2secthetacsctheta$
In the exercises below, findan equation in rectangular coordinates that has the samegraph as the given equation in polar coordinates.
Ex 10.1.21$ds r=sin(3theta)$(answer)
Ex 10.1.22$ds r=sin^2theta$(answer)
Ex 10.1.23$ds r=secthetacsctheta$(answer)
Ex 10.1.24$ds r=tantheta$(answer)
